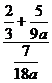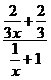Level D Review Packet
This packet briefly reviews the topics covered
on the Level D Math Skills Assessment.
If you need additional study resources and/or assistance with any of the
topics below, please visit the Math Center during our hours of operation, Monday
– Thursday 9am – 7pm and Friday 9am – 12pm.
All questions and concerns about the assessment should
be directed to Rebecca Tiffin, Math Center Director. Professor Tiffin can be contacted by phone at
385-7395 or e-mail at rtiffin@sjfc.edu.
Note:
A calculator is not
allowed on the Level D Math Skills Assessment.
|
Solving
Equations |
|
|
1)
Solve for
x: |
2) Solve for x: 3(3x – 6) = 3(x – 2) |
|
3) Solve for x: -6x + 1 = 3(2x +1) |
4) Solve for x: 3(2x – 3) + 5 = 20 – 2x |
|
5) Solve for x: 7x – 8 = 2(3 + 2x) + 4 |
6)
Solve for x: |
|
7)
Solve for x: |
8)
Solve for x: |
|
Solving
Equations - decimal
coefficients and constants |
|
|
1) Solve for m:
|
2) Solve for m: |
|
3) Solve for m: |
4) Solve for m:
|
|
Solving
Inequalities |
|
|
1)
Solve: 14 |
2)
Solve:
2x - 4 |
|
3)
Solve:
2(x – 4) - 3 > 3x + 22 |
4)
Solve:
3(x – 2) > 7 - 4x |
|
Evaluating
Expressions - negative and fractional exponents |
|
|
1)
What is the value of |
2)
What is the value of |
|
3)
What is the value of |
4)
What is the value of |
|
Solving
Equations – variables
in the exponent |
|
|
1)
1) Solve for x: |
2) Solve for x: |
|
2)
3) Solve for
x: |
4) Solve for x: |
|
Solving
Radical Equations |
|
|
1) Find the solution set of |
2) Find the solution set of |
|
3) Find the solution set of |
4) Find the solution set of |
|
Solving
Absolute Value Equations |
|
|
1) Find the solution set of |x – 6| = 6. |
2) Find the solution set of |2 – 4x| = 12. |
|
3) Find the solution set of |7x – 4| = 3. |
4) Find the solution set of |3 – 2x| = 13. |
|
Solving
for a Variable |
|
|
1)
Solve in terms of y:
|
2)
Solve in terms of y:
|
|
3)
Solve in terms of y:
|
4)
Solve in terms of y:
|
|
Multiplying
Polynomials |
|
|
1) Multiply: (3x + 4)(2x – 3) |
2)
Multiply: (4x – 3y)(2x – y) |
|
3)
Multiply:
(x + 6)2 |
4)
Multiply:
(2x - 3)2 |
|
Factoring |
|
|
1)
Factor completely:
|
2)
Factor completely:
|
|
3)
Factor completely:
|
4)
Factor completely:
|
|
Solving
Quadratic Equations |
|
|
1)
Solve: |
2)
Solve: |
|
3)
Solve: |
4)
Solve: |
|
Solving
Systems of Linear Equations |
|
|
1) What is the solution to the system of equations below? x – y = 8 x + y = 2 |
2) What is the solution to the system of equations below? –x + y = 3 x + y = 5 |
|
3) What is the solution to the system of equations below? x + y = 7 -x
+ y = 3 |
4) What is the solution to the system of equations below? 2x – y = 1 -2x
+ 3y = 5 |
|
5) What is the solution to the system of equations below? x
– 2y = 2 x
+ 2y = -14 |
6) What is the solution to the system of equations below? x + 3y = 12 2x
– 3y = 6 |
|
7) What is the solution to the system of equations below? -3x
+ y = 8 3x – 2y = -10 |
8) What is the solution to the system of equations below? x + 2y = -2 3x
+ 2y = -12 |
|
Dividing
Polynomials |
|
|
1) Find
the quotient when 6x2+12x3
is divided by -6x2. |
2) Find the quotient when 4a2x – 8ax+12ax2 is divided by 4ax. |
|
3)
Simplify completely:
|
4)
Simplify completely:
|
|
5)
Simplify completely:
|
6)
Simplify completely:
|
|
7)
Simplify completely:
|
8)
Simplify completely:
|
|
Adding
and Subtracting Algebraic Fractions |
||
|
1) Express as a single fraction in lowest terms: |
2) Express as a single fraction in lowest terms: |
|
|
3) Express as a single fraction in lowest terms: |
4) Express as a single fraction in lowest terms: |
|
|
5) Express as a single fraction in lowest terms:
|
6) Express as a single fraction in lowest terms: |
|
|
7) Express as a single fraction in lowest terms: |
8) Express as a single fraction in lowest terms: |
|
|
Multiplying
Algebraic Fractions |
|
|
1) Write the following expression in simplest form: |
2) Write the following expression in simplest form:
|
|
3) Write the following expression in simplest form: |
4) Write the following expression in simplest form:
|
|
5) Write the following expression in simplest form: |
6) Write the following expression in simplest form:
|
|
7) Write the following expression in simplest form: |
8) Write the following expression in simplest form:
|
|
Equations
Involving Fractions |
|
|
1) Solve for all values of x: |
2) Solve for all values of x: |
|
3) Solve for all values of x: |
4) Solve for all values of x: |
|
Simplifying
Complex Fractions |
|
|
1)
Simplify: |
2)
Simplify: |
|
3)
Simplify: |
4)
Simplify: |
|
Finding
Inverses Algebraically |
|
|
1) What
is the inverse of the function |
2) What
is the inverse of the function |
|
3) What
is the inverse of the function |
4) What
is the inverse of the function |
|
Domain |
|
|
1) What
is the domain of the function |
2) What
is the domain of the function |
|
3) What
is the domain of the function |
4) What
is the domain of the function |
|
Composition |
|
|
1)
Given: Find: |
2)
Given: Find: |
|
3)
Given: Find: |
4)
Given: Find: |
|
5)
Given: Find: |
6)
Given: Find: |
|
7)
Given: Find: |
8)
Given: Find: |
|
Logarithms |
|
|
1)
Solve for x: |
2)
Solve for x: |
|
3)
Solve for x: |
4)
Solve for x: |
|
5)
Solve for x:
|
6)
Solve for x:
|
|
7)
Solve for x: |
8)
Solve for x: |
|
9)
Solve for x: |
10) Solve
for x: |
|
11) Solve
for x: |
12) Solve
for x: |
|
Log
Equations |
|
|
1) Solve for x: log2(x) + log2(x – 2) = 3 |
2) Solve for x: log3(x + 3) + log3(x + 5) = 1 |
|
3) Solve for x: log3(x - 2) - log3(x - 4) = 2 |
4) Solve for x : log5(x) – log5(x – 2) = 1 |
|
Trigonometry |
|
|
1)
What value for x in the interval |
2)
What value for x in the interval |
|
3) If |
4) If |
|
5) If |
6) If
|