Brief introduction to

Since Gauss proved the Fundamental Theorem of Algebra, we know that all complex numbers are of the form x + yi, where x and y are real numbers, real numbers being all those numbers which are positive, negative, or zero. Therefore, we can use the xy-plane to display complex numbers. We'll even call it the complex plane when we use the xy-plane that way. That gives us a second way to complex numbers, the first way being algebraically as in the expression x + yi.

Notation. The standard symbol for the set of all complex numbers is C, and we'll also refer to the complex plane as C.

We'll try to use x and y for real variables, and z and w for complex variables. For example, the equation z = x + yi is to be understood as saying that the complex number z is the sum of the real number x and the real number y times i. In general, the x part of a complex number z = x + yi is called the real part of z, while y is called the imaginary part of z. (Sometimes yi is called the imaginary part.)

When we use the xy-plane for the complex plane C, we'll call the x-axis by the name real axis, and the y-axis we'll call the imaginary axis.

Real numbers are to be considered as special cases of complex numbers; they're just the numbers x + yi when y is 0, that is, they're the numbers on the real axis. For instance, the real number 2 is 2 + 0i. The numbers on the imaginary axis are sometimes called purely imaginary numbers. An important concept for numbers, either real or complex is that of absolute value. Recall that the absolute value |x| of a real number x is itself, if it's positive or zero, but if x is negative, then its absolute value |x| is its negation –x, that is, the corresponding positive value. For example, |3| = 3, but |–4| = 4. The absolute value function strips a real number of its sign.

For a complex number z = x + yi, we define the absolute value |z| as being the distance from z to 0 in the complex plane C. This will extend the definition of absolute value for real numbers, since the absolute value |x| of a real number x can be interpreted as the distance from x to 0 on the real number line.

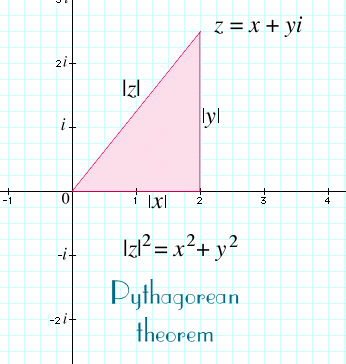We can find the distance |z| by using the Pythagorean theorem. Consider the right triangle with one vertex at 0, another at z and the third at x on the real axis directly below z (or above z if z happens to be below the real axis). The horizontal side of the triangle has length |x|, the vertical side has length |y|, and the diagonal side has length |z|. Therefore,

(Note that for real numbers like x, we can drop absolute value when squaring, since |x|² = x².) That gives us a formula for |z|, namely,

The unit circle. Some complex numbers have absolute value 1. Of course, 1 is the absolute value of both 1 and –1, but it's also the absolute value of both i and –i since they're both one unit away from 0 on the imaginary axis. The unit circle is the circle of radius 1 centered at 0. It include all complex numbers of absolute value 1, so it has the equation |z| = 1.

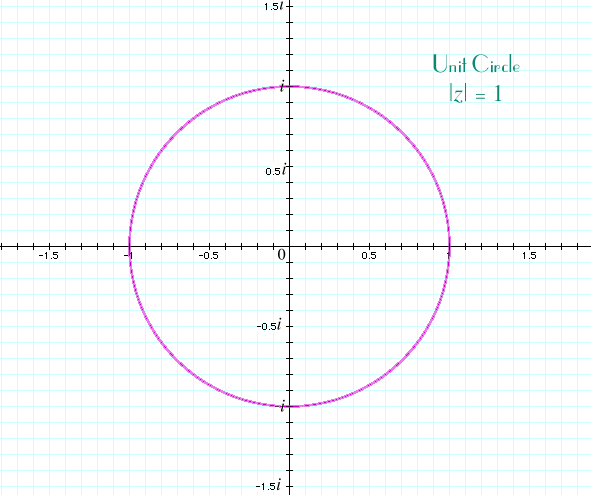
A complex number z = x + yi will lie on the unit circle when x² + y² = 1. Some examples, besides 1, –1, i, and –1 are ±√2/2 ± i√2/2, where the pluses and minuses can be taken in any order. They are the four points at the intersections of the diagonal lines y = x and y = x with the unit circle.

Multiplication done algebraically. Complex multiplication is a more difficult operation to understand from either an algebraic or a geometric point of view. Let's do it algebraically first, and let's take specific complex numbers to multiply, say 3 + 2i and 1 + 4i. Each has two terms, so when we multiply them, we'll get four terms:

Now the 12i + 2i simplifies to 14i, of course. What about the 8i²? Remember we introduced i as an abbreviation for √–1, the square root of –1. In other words, i is something whose square is –1. Thus, 8i² equals –8. Therefore, the product (3 + 2i)(1 + 4i) equals –5 + 14i.

If you generalize this example, you'll get the general rule for multiplication

Remember that (xu – yv), the real part of the product, is the product of the real parts minus the product of the imaginary parts, but (xv + yu), the imaginary part of the product, is the sum of the two products of one real part and the other imaginary part.

Let's look at some special cases of multiplication.

Multiplication and absolute value. Even though we've only done one case for multiplication, it's enough to suggest that the absolute value of zw (i.e., distance from 0 to zw) might be the absolute value of z times the absolute value of w. It was when w was the real number u just above. In fact, this is true in general:

The verification of this identity is an exercise in algebra. In order to prove it, we'll prove it's true for the squares so we don't have to deal with square roots. We'll show |zw|² = |z|²|w|². Let z be x + yi, and let w be u + vi. Then, according to the formula for multiplication, zw equals (xu – yv) + (xv + yu)i. Recall that we defined absolute value by:

Similarly, we have

and, since zw = (xu – yv) + (xv + yu)i,

So, in order to show |zw|² = |z|²|w|², all you have to do is show that

and that's a straightforward exercize in algebra. Note that the red expression (above) follows from

Roots of unity. The various roots of 1 are called roots of unity. In general, by the Fundamental Theorem of Algebra, the number of n-th roots of unity is n, since there are n roots of the n-th degree equation z^u – 1 = 0. The square roots of unity are 1 and –1. The fourth roots are ±1, ±i, . Note that ±√2/2 ± i√2/2 are square roots of i and –i, and now with the formula for multiplication, that's easy to verify. Therefore, the eight eight-roots of unity are ±1, ±i, and ±√2/2 ± i√2/2. Notice how these eight roots of unity are equally spaced around the unit circle.

We can use geometry to find some other roots of unity, in particular the cube roots and sixth roots of unity. But let's wait a little bit for them.

You can analyze what multiplication by –i does in the same way. You'll find that multiplication by –i gives a 90° clockwise rotation about 0. When we don't specify counterclockwise or clockwise when referring to rotations or angles, we'll follow the standard convention that counterclockwise is intended. Then we can say that multiplication by –i gives a –90° rotation about 0, or if you prefer, a 270° rotation about 0.

A geometric interpretation of multiplication. To completely justify what we're about to see, trigonometry is needed, and that is done in an optional section. For now, we'll see the results without the justification. We've seen two special cases of multiplication, one by reals which leads to scaling, the other by i which leads to rotation. The general case is a combination of scaling and rotation.

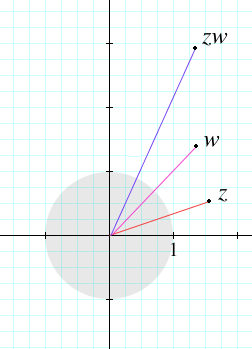
Let z and w be points in the complex plane C. Draw the lines from 0 to z, and 0 to w. The lengths of these lines are the absolute values |z| and |w|, respectively. We already know the length of the line from 0 to zw is going to be the absolute value |zw| which equals |z| |w|. (In the diagram, |z| is about 1.6, and |w| is about 2.1, so |zw| should be about 3.4. Note that the unit circle is shaded in.) What we don't know is the direction of the line from 0 to zw.

The answer is that "angles add". We'll determine the direction of the line from 0 to z by a certain angle, called the argument of z, sometimes denoted arg(z). This is the angle whose vertex is 0, the first side is the positive real axis, and the second side is the line from 0 to z. The other point w has angle arg(w). Then the product zw will have an angle which is the sum of the angles arg(z) + arg(w). (In the diagram, arg(z) is about 20°, and arg(w) is about 45°, so arg(zw) should be about 65°.)

In summary, we have two equations which determine where zw is located in C:

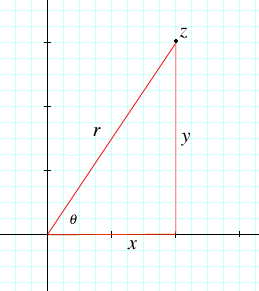
Polar coordinates will help us understand complex numbers geometrically. On the one hand, the usual rectangular coordinates x and y specify a complex number z = x + yi by giving the distance x right and the distance y up. On the other hand, polar coordinates specify the same point z by saying how far r away from the origin 0, and the angle for the line from the origin to the point. We've already called the distance r the absolute value |z| of z, and we saw how the Pythagorean theorem gave relation between it and x and y:

Next, we need to deal with the angle . We'll follow the standard convention for specifying the angle . This convention takes the positive x-axis (our real axis) to be at angle 0°, the positive y-axis (our imaginary axis) at angle 90°, the negative x-axis angle 180°, and the negative y-axis at angle 270°. Also, 360° can be added or subtracted from any angle and the direction is not changes. So, 0°, 360°, 720°, and –360° all refer to the positive x-axis. Similarly, 270° and –90° both refer to the negative y-axis. A 45° angle runs along the line y = x, up to the right. And so forth.

A point z can be specified by either pair, the pair of rectangular coordinates, x and y, or the pair of polar coordinates, r, which is |z|, and , which is arg (z). Since either pair determines the point, each pair should determine the other pair. There should be four equations, connecting them, and so there are. The Pythagorean identity was mentioned above, but the others require trigonometry. From the same triangle we used for the Pythagorean theorem, we find the following three relations:

tan = y/x,   x = r cos , and   y = r sin .

Now, if we apply these relations to our complex number z = x + yi, then we get an alternate description for z

z	=	x + iy
	=	r cos + i r sin
	=	r (cos + i sin )
	=	|z| (cos + i sin )

Note that the complex number cos  + i sin  has absolute value 1 since cos² + sin² equals 1 for any angle . Thus, every complex number z is the product of a real number |z| and a complex number cos  + i sin .

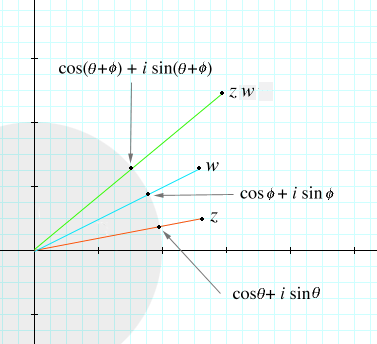
We're almost to the point where we can prove the last unproved statement of the previous section on multiplication, namely, that arg(zw) = arg(z) + arg(w). As above, we take arg(z) to be , and now let arg(w) be . Then,

z = |z| (cos + i sin )

w = |w| (cos + i sin )

We need to show that arg(zw) is  + . In other words

zw = |zw| (cos ( + ) + i sin ( + ))

If we use the addition formulas for cosine and sine at one crucial point, we'll have it. Recall from trigonometry these addition formulas:

cos ( + ) = cos   cos  – sin  sin 

sin ( + ) = cos  sin  + sin  cos .

Now we're ready to show arguments add in the product zw.

zw	=	|z| (cos + i sin ) |w| (cos + i sin )
	=	|zw| (cos + i sin ) (cos + i sin )
	=	|zw| ((cos   cos  – sin  sin ) + i(cos  sin  + sin  cos ))
	=	|zw| (cos ( + ) + i sin ( + ))

Thus, arg(zw) is  + , as claimed.

I repeat, this material is directly derived from pages located at http://www.clarku.edu/~djoyce/complex/