The following
diagram provides a neat and not well known proof that the square root of 2 is
irrational. (This proof is by Tom Apostol, NOT ME. It is here because I like it. The wording is mine.)
Here are the
details. Suppose ![]() is rational then
is rational then ![]() =m/n for some integers m and n. Let n be the smallest integer
for which there is an m with
=m/n for some integers m and n. Let n be the smallest integer
for which there is an m with ![]() =m/n.
=m/n.
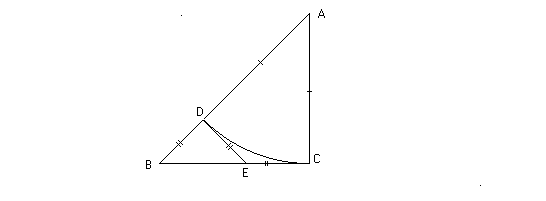
Let ABC be an
isosceles right triangle with side n. In the above diagram,
length(AC)=length(BC)=n . And length(AB)=m= n![]() . Now consider a circle, O, with center at A and radius equal
to length(AC) or n. At point D, the intersection of O with AB, we erect a
perpendicular which intersects BC at E. Note that since DE and EC are tangents
to circle O, they are equal. But DE is equal to BD and BD is an integer (namely
m-n). But then EC is also the integer m-n and then BE is an integer (namely
2n-m) . Since BED is a 45-45-90 triangle with integer sides we now have a
contradiction to the choice of n as the smallest integer for which there is an
m with
. Now consider a circle, O, with center at A and radius equal
to length(AC) or n. At point D, the intersection of O with AB, we erect a
perpendicular which intersects BC at E. Note that since DE and EC are tangents
to circle O, they are equal. But DE is equal to BD and BD is an integer (namely
m-n). But then EC is also the integer m-n and then BE is an integer (namely
2n-m) . Since BED is a 45-45-90 triangle with integer sides we now have a
contradiction to the choice of n as the smallest integer for which there is an
m with ![]() =m/n. (length(DE)<length(BE)<length(BC)=n)
=m/n. (length(DE)<length(BE)<length(BC)=n)